North Dakota State
Fall 2017
The Graduate Colloquium is a colloquium series presented primarily by graduate students. Any graduate student or faculty member is welcome to present research or other mathematical topics of interest. Talks are intended to be accessible to all graduate students, though everyone is welcome to attend. Talks are generally given on Thursday from 3:00pm to 4:00 in Minard 214. Coffee and treats are served at each meeting.
Upcoming Talks
Speaker: Faraad Armwood
Date(s): 9/14/17
Title: "What's the best way to eat a slice of pizza"
Abstract: This will be a two part talk. The goal of this talk is to see if curvature is an intrinsic property. This remarkable result was shown by Gauss. It says that the Gaussian curvature of a surface is invariant under isometric embedding i.e the Gaussian curvature doesn't change if you deform your surface by just bending and twisting. Below you will find an animation showing that the Helicoid and the Catenoid are isometric surfaces.
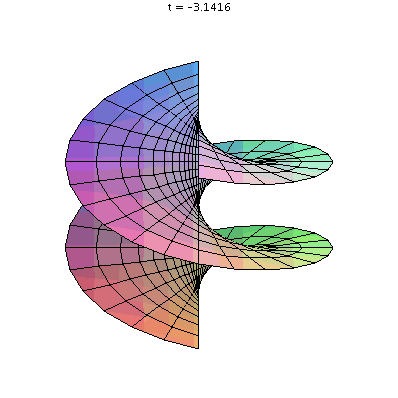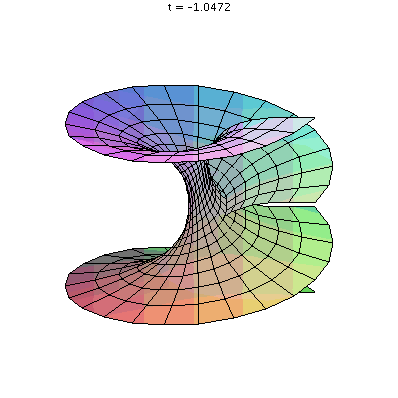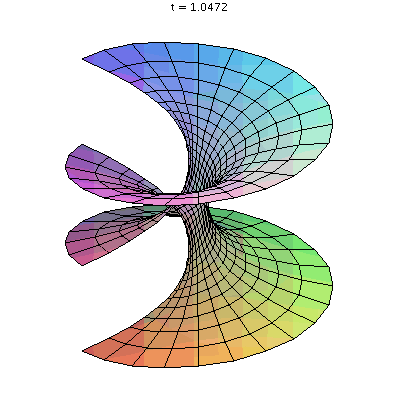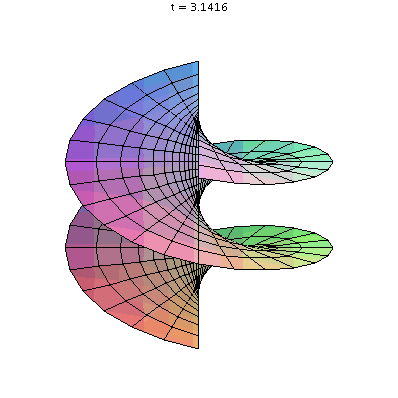
Speaker: Sara Solhjem
Date: 9/21/17
Title: "Sign Matrix Polytopes"
Abstract: I will be giving a basic look into my research, the fun world of Combinatorics! We will look at different tableau and how they are related to certain rectangular matrices with entries of 0, 1 and -1. Then we will talk about what a polytope is and why they are studied. Finally, we put all this together to look at the polytopes that I have been studying and all the things you can count on them. This is also a practice talk for a job interview and it will be accessible for undergrads. Please come and feel free to give me feedback!
Speaker: Dr. Bjorn Berntson
Date: 10/12,19/17
Title: "Integrability in mathematical physics"
Abstract: The notion of an integrable system is rooted in Hamiltonian mechanics, but today extends to encompass a wide variety of physically-relevant systems in settings far removed from its classical origins. Despite this, there is no universal definition of integrability. In this pair of talks, I will discuss some commonly recognizable features of integrability in classical and quantum mechanical models, ordinary and partial differential equations, and discrete and functional equations.

Speaker: Dr. Barabanov
Date: 10/26,11/2
Title: "Second order differential equations and classical orthogonal functions"
Abstract:We consider polynomial solutions of second order linear differential equations on interval, ray and line. Using the Rodrigues’ formula we introduce Jacobi, Laguerre and Hermite polynomials. We’ll study some properties of these polynomials. Then we establish relations of these polynomials with Gauss quadrature and eigenfunctions of certain boundary value problems, for example, for the Schrodinger equation.