MATH 160
EXAM 3
- (25 pt) Find the following limits
a)  b)
b) 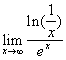 c)
c)  d)
d) 
e)
- (20 pt) Find the absolute maximum and minimum values of
 on [2,4].
on [2,4].
- (15 pt) a) If you have two functions
 and
and 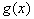 such that
such that  then what can you say about the relationship between
then what can you say about the relationship between 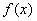 and
and  ?
?
b) Find  where
where 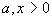 and
and  is a constant.
is a constant.
c) Use the results from a) and b) to show that  .(Hint, plug in 1).
.(Hint, plug in 1).
- (20 pt) For the following functions sketch the graphs. You should make clear where local extrema, points of inflection, intervals of increase/decrease, concavity, and asymptotes are.
a)  b)
b) 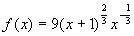
5. (20 pt) You are given the following information about the function 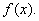
 ,
, 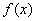 is continuous,
is continuous,  when
when  and when
and when 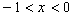 ,
, 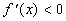 when
when  and when
and when 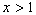 ,
,  when
when  and when
and when 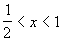 and
and  when
when  and when
and when 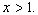 You may assume that –1, 0, and 1 are critical numbers.
You may assume that –1, 0, and 1 are critical numbers.
- Where (if anywhere) do the local extrema occur (and what kind of extrema are they)?
- Where (if anywhere) do points of inflection occur?
- At which of the critical points is it not possible to have derivative 0?(Justify)
- In which direction is it possible to have a horizontal asymptote? (Justify)
- Sketch the graph of a function that satisfies the above conditions.
- Bonus (5 pt) Sketch the graph of a function that has a point on its graph that is both a local minimum and a point of inflection. Circle the point.
- Bonus (5 pt)
 is continuous on [-1,1] and
is continuous on [-1,1] and 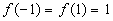 . But there is no place on the function where
. But there is no place on the function where 
Does this contradict Rolle’s Theorem (why)?
![]() b)
b) 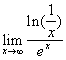 c)
c) ![]() d)
d) ![]()
![]()
![]() where
where ![]() and
and ![]() is a constant.
is a constant.![]() .(Hint, plug in 1).
.(Hint, plug in 1).![]() b)
b) 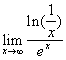 c)
c) ![]() d)
d) ![]()
![]()
![]() where
where ![]() and
and ![]() is a constant.
is a constant.![]() .(Hint, plug in 1).
.(Hint, plug in 1).![]() b)
b) ![]()
![]()
![]() ,
, ![]() is continuous,
is continuous, ![]() when
when ![]() and when
and when ![]() ,
, ![]() when
when ![]() and when
and when ![]() ,
, ![]() when
when ![]() and when
and when ![]() and
and ![]() when
when ![]() and when
and when ![]() You may assume that –1, 0, and 1 are critical numbers.
You may assume that –1, 0, and 1 are critical numbers.