MATH 160
FINAL EXAM
- (24 pt) Find the following limits:
a) 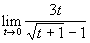 b)
b)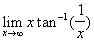 c)
c) 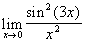 d)
d)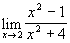
e) 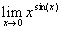 f)
f) 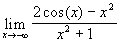
- (5 pt) Use the definition of the derivative to find the derivative of
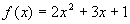 .
.
- (20 pt) Find the derivative for the following functions
a) 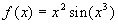 b)
b) 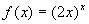 c)
c) 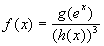 d)
d) 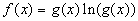
- (8 pt) A particle takes off from the ground (s(0)=0) and has initial velocity 1 (v(0)=1). Its acceleration is given by a(t)=cos(t) for t ³
0. Find the position function of the particle for t ³
0 and sketch it.
- (5 pt) Use either differentials or Newton’s Method to estimate
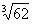 .
.
- (6 pt) Find the maximum and minimum values of the function
 on the interval [-1,2].
on the interval [-1,2].
- (10 pt) A plane flies at a constant height of 3 miles above the ground at velocity of 200 mi/hr. The flight path takes the plane directly over a radar station on the ground. How fast is the distance between the plane and the station changing when the plane is 5 miles from the station?
- (6 pt) Use the definition of the definite integral to evaluate
 . Use the Fundamental Theorem of Calculus to check your answer.
. Use the Fundamental Theorem of Calculus to check your answer.
- (10 pt) Sketch the function
 . Make note of local max/min values, points of inflection, and asymptotes.
. Make note of local max/min values, points of inflection, and asymptotes.
- (6 pt) Use implicit differentiation to find the tangent line to
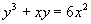 at the point (-1,2).
at the point (-1,2).
- (Bonus 5pt) Show that among all rectangles of fixed area A, a square has the smallest perimeter.
(Bonus 5pt) The picture of the following function. Where is the function continuous? Where is it differentiable? Sketch the derivative.
![]() b)
b)![]() c)
c) ![]() d)
d)![]()
![]() f)
f) ![]()
![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
![]() b)
b)![]() c)
c) ![]() d)
d)![]()
![]() f)
f) ![]()
![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()