Math 420/620
Problem Set 1
Prove Proposition 0.1 from the notes. That is, let 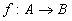 be a function.
be a function.
- Show that
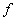 is one to one
is one to one 
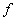
has a left inverse.
- Show
 is onto
is onto 
 has a right inverse.
has a right inverse.
- Show
 is bijective
is bijective 

 such that
such that  and
and 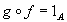
.
- Let
 and
and  be finite sets with
be finite sets with  and let
and let 
be a function. Show the following conditions are equivalent.
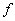 is bijective.
is bijective.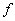 is one-to-one.
is one-to-one.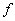
is onto.
- Let

be a nonempty set.
- If
 is an equivalence relation on
is an equivalence relation on 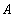 , then the set of equivalence classes of
, then the set of equivalence classes of  form a partition of
form a partition of 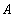 .
.
- If
 is a partition of
is a partition of  then there is an equivalence relation on
then there is an equivalence relation on  whose equivalence classes are precisely the sets
whose equivalence classes are precisely the sets 
.
- Let
 and
and 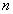 be nonzero integers whose greatest common divisor is the integer
be nonzero integers whose greatest common divisor is the integer  . Show that there are integers
. Show that there are integers  and
and 
such that

![]()