Math 420/620
Fall 1999
Homework 3
- Given elements
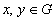 , we define the commutator
, we define the commutator 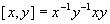 . If
. If  , then for all
, then for all  ,
, 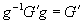 .
.
- Consider the group generated by the elements
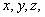 and
and 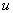 subject to the relations
subject to the relations

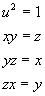
This group is denoted  and is called the quaternion group.
and is called the quaternion group.
Show that 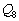 is a nonabelian group of order 8.
is a nonabelian group of order 8.
- Consider the following two groups:
- G is generated (multiplicatively) by the real matrices
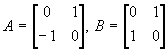
- H is generated (multiplicatively) by the complex matrices
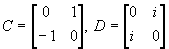
- Show that G and H are nonabelian groups of order 8.
- Show that precisely one of G and H is isomorphic to
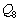
.
- Find all subgroups of symmetric group on three elements.
- We define
 =
=
.
- Show that for any group
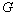 ,
, 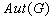 is itself a group.
is itself a group.
- Show that if we define
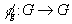 by
by 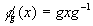 , then
, then 
- Show that the map
 is a homomorphism from
is a homomorphism from  to
to 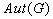 .
.
- Let
 . Compute the number of elements in
. Compute the number of elements in 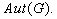 (
(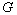
is called an elementary abelian p-group).
![]()
![]()
![]() and is called the quaternion group.
and is called the quaternion group.![]() is a nonabelian group of order 8.
is a nonabelian group of order 8.![]()
![]()
![]() and is called the quaternion group.
and is called the quaternion group.![]() is a nonabelian group of order 8.
is a nonabelian group of order 8.![]()
![]()