Math 420/620
Homework 5
Fall 1999
- If
 has finite index
has finite index  in the group
in the group  , then show that there is a normal subgroup
, then show that there is a normal subgroup 
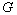 , with
, with 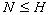 and
and 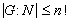 .
.
- Classify all groups of order
 with
with  a nonzero prime number.
a nonzero prime number.
- Let
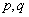 be distinct odd primes with
be distinct odd primes with 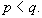
- Assume that
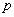 does not divide
does not divide  , classify all groups of order
, classify all groups of order 
- (G)
Classify all groups of order 
without the above assumption.
- Let
 be a group of order
be a group of order 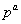 for a nonzero prime
for a nonzero prime  . Prove that
. Prove that  has subgroups of or
der
has subgroups of or
der  for all
for all 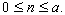
- How many elements of order 7 must a simple group of order 168 have?
- If
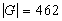 , 2907, or 6545, show that
, 2907, or 6545, show that  is not simple.
is not simple.
- (G)
Let 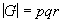 with
with 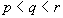 distinct primes. Show
distinct primes. Show  is not simple.
is not simple.
- (G)
Show if  is a
nonabelian simple group of order less than 100, then
is a
nonabelian simple group of order less than 100, then 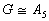
.