Math 420/620

Fall 1999

Homework 6

 

  1. Construct every semidirect product of with itself.

    2.  

  2. Show that (where 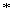denotes semidirect product).

    3.  

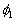  3. (G) Assume that is cyclic, is arbitrary and and 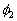are homomorphisms from into 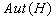such that and are conjugate subgroups of Show that .

    4.  

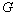  4. Let be a -group of order for some . Show that for all ,

    5.  

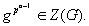
  5. Classify all groups of order:
  1. 12.
  2. (G) 18.

 

  1. Find all abelian groups of order 2160.

    2.  

  2. Give an example of a finite nonabelian group that cannot be written as a semidirect product of two of its proper subgroups.

    3.  

  3. (G) Classify all groups of order for any prime