Math 420/620
Homework 7
- a) Let
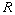 be a Boolean ring (that is,
be a Boolean ring (that is, 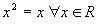 ). Show that
). Show that 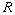 is commutative.
is commutative.
b) (G) Give an example of a Boolean ring that has no identity.
- Let
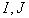 be (left) ideals of
be (left) ideals of 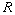 . Show that
. Show that  is also a (left) ideal.
is also a (left) ideal.
- Assume that
 is a ring homomorphism with
is a ring homomorphism with 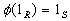 . Show that
. Show that 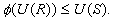
- Show that if
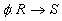
is a homomorphism of rings then:
 is an ideal of
is an ideal of 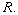
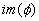 is a subring of
is a subring of 
- Find all possible rings with:
- 2 elements.
- (G)
4 elements.
- Let
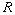
be a commutative ring with 1.
- Show any maximal ideal M, is a prime ideal.
- (G)
If 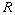
is finite, show that any prime ideal is maximal.