Math 420/620
Exam 1
Fall 1999
- (Fermatís Little Theorem) Prove that if
 is a nonzero prime number and
is a nonzero prime number and  is any integer, then
is any integer, then 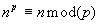 .
.
- Let
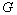 be a group and define the mapping
be a group and define the mapping 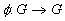 by
by 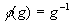
.
- Show that
 is an automorphism of
is an automorphism of 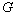 if and only if
if and only if 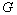 is abelian.
is abelian.
- Use part a) to show that if
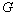 is a finite abelian group and
is a finite abelian group and 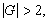 then
then 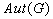
is a finite group of even order.
- Let
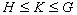 . Prove that
. Prove that 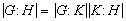 .
.
- Assume that
 is a group of finite order and
is a group of finite order and  is a normal subgroup of
is a normal subgroup of 
.
- If
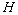 is a subgroup of
is a subgroup of 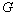 with
with 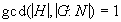 , then
, then 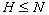 .
.
- Use part a) to show that if
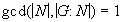 , then
, then 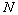 is the unique subgroup of
is the unique subgroup of 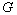 of order
of order 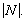
- (G)
Classify all groups of order 2p with p a prime integer.
6. (G) Find a formula expressing the number of distinct abelian groups of order  where
where  is a prime number.
is a prime number.
![]() where
where ![]() is a prime number.
is a prime number.