Math 420/620
Fall 1999
Exam 2
(You may assume that all rings are commutative with identity.)
- Consider the ring of rational integers Z .
- Prove that Z is a principal ideal domain (PID).
- Show that the polynomial ring Z[x] is not a PID.
- Let
 be a homomorphism of commutative rings (you may assume that
be a homomorphism of commutative rings (you may assume that 
).
- Show that if
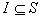 is an ideal, then
is an ideal, then 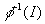 is an ideal of
is an ideal of 
- Show that if
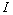 is prime, then so is
is prime, then so is 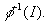
- Let
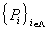 be a family of prime ideals in
be a family of prime ideals in 
- Show that
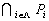 is a radical ideal of
is a radical ideal of 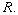
- (G) Show that if
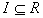 is a radical ideal, then
is a radical ideal, then 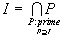
.
- The nilradical of
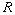 is the collection of all nilpotent elements of
is the collection of all nilpotent elements of 
.
- Show that the nilradical is an ideal of

- (G) Show that the nilradical is the intersection of all prime ideals of
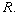
- The Jacobson radical (
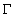 ) of
) of 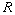 is the intersection of all maximal ideals of
is the intersection of all maximal ideals of 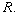
- Show that the following conditions are equivalent:
 .
. is a unit of
is a unit of  for all
for all 
- Show that the nilradical is always contained in the Jacobson radical.
- Compute the nilradical and the Jacobson radical for the rings Z, Z12.
- (G) Show that if
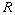
is finite, then the Jacobson radical and the nilradical are the same.