Math 420/620
Fall 1999
Final Exam
- Let
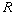 be a UFD, show that
be a UFD, show that 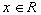 is irreducible if and only if it is prime.
is irreducible if and only if it is prime.
- Consider the ring Z
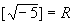 . We define the norm map
. We define the norm map 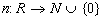 by
by 
. Show the norm has the following properties:
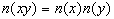 for all
for all 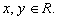
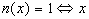 is a unit in
is a unit in 
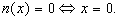
Use these facts to show that the ring Z is not a UFD.
is not a UFD.
- Show the following conditions are equivalent:
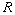 is a PID
is a PID is a UFD and every nonzero prime ideal of
is a UFD and every nonzero prime ideal of 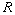
is maximal.
- a) Construct an example of a ring that has precisely
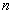 maximal ideals.
maximal ideals.
b) (G) If your example from a) is not a domain, then make a new example which is a domain (reverse the instructions if your example from a) is a domain).
- Consider that the polynomial ring
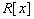
. Show that the following conditions are equivalent.
 is a PID
is a PID is a Euclidean domain
is a Euclidean domain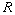
is a field.
- (G)
Let 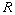 be a domain with quotient field
be a domain with quotient field  We say that
We say that 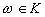 is integral if
is integral if 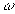 is a root of a monic polynomial with coefficients in
is a root of a monic polynomial with coefficients in 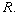 Show that if
Show that if  is a UFD and
is a UFD and 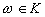 is integral, then
is integral, then 
- Let
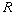 be commutative with identity. Let
be commutative with identity. Let 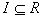 be any ideal and let
be any ideal and let  . Show that
. Show that 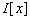 is an ideal of
is an ideal of 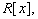 and that
and that 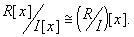
![]() is not a UFD.
is not a UFD.