Math 421/621
Spring 2000
Homework 1
- Prove that if A is an R-algebra, then A is an R-module.
- a) Let F be any field. Find all F-submodules of F and find all quotient modules of F.
b) Do the same as in part a), replacing the field "F" with the integers Z.
- Let M, N, K be
 -modules. If
-modules. If 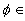
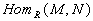 and
and 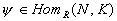 then
then  Use this to show that
Use this to show that 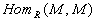 is a ring with identity.
is a ring with identity.
- Let
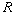 be a commutative ring
with 1,
show that
be a commutative ring
with 1,
show that  as left
as left 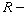 modules.
modules.
- Let
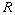 be commutative with 1. Show that
be commutative with 1. Show that  as rings. (G) See if you can find a counterexample to #10, pg. 331.
as rings. (G) See if you can find a counterexample to #10, pg. 331.
- (G)
Find 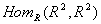 where
where 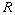
denotes the real numbers. Characterize the elements that are isomorphisms.
 Use this to show that
Use this to show that  Use this to show that
Use this to show that